Sign-up for free online course on ANSYS simulations!Author: Rajesh Bhaskaran and Yong Sheng Khoo, Cornell University
Problem Specification
1. Create Geometry in GAMBIT
2. Mesh Geometry in GAMBIT
3. Specify Boundary Types in GAMBIT
4. Set Up Problem in FLUENT
5. Solve!
6. Analyze Results
7. Refine Mesh
Problem 1
Problem 2
Step 7: Refine Mesh
It our mesh refine enough? Will the current mesh give us an accurate representation of the physical flow? Mesh density determine the truncation error of our simulation. With too little mesh density, the result we obtain will be inaccurate. With too many mesh elements, we will be wasting unnecessary computational power (long computational time!). To get the optimum mesh density, we do mesh sensitivity analysis.
For this purpose, we will create three model with different mesh density. We will create a coarser mesh and a finer mesh and compare all the three meshes together.
For coarse mesh, reduce the mesh density by half of the original mesh. For fine mesh, double the mesh density compared to the original density.
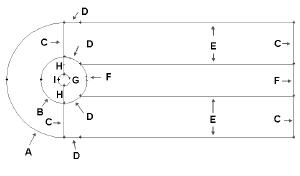
Follow Step 1 through Step 5. At step 2, use the following edge mesh properties instead.
Label |
Medium Mesh (Original) |
Coarse Mesh |
Fine Mesh |
A |
Interval Count: 36, Double First Length: 0.5 |
Interval Count: 24, Double First Length: 0.7 |
Interval Count: 54, Double First Length: 0.3 |
B |
Interval Count: 36, Double First Length: 0.2 |
Interval Count: 24, Double First Length: 0.3 |
Interval Count: 54, Double First Length: 0.12 |
C |
Interval Count: 30, First Length: 0.1 |
Interval Count: 20, First Length: 0.2 |
Interval Count: 45, First Length: 0.09 |
D |
Interval Count: 18 |
Interval Count: 12 |
Interval Count: 27 |
E |
Interval Count: 90, First Length: 0.1 |
Interval Count: 60, First Length: 0.15 |
Interval Count: 135, First Length: 0.07 |
F |
Interval Count: 36 |
Interval Count: 24 |
Interval Count: 54 |
G |
Interval Count: 72 |
Interval Count: 48 |
Interval Count: 108 |
H |
Interval Count: 30 |
Interval Count: 20 |
Interval Count: 45 |
I |
Interval Count: 36, Double First Length: 0.05 |
Interval Count: 24, Double First Length: 0.07 |
Interval Count: 54, Double First Length: 0.03 |
To double the mesh density, the interval count is increased by factor of 1.5. The first length is decreased by a factor of about 1.5. To half the mesh density, the interval count is decreased by factor of 1.5. The first length is increased by a factor of about 1.5. Think about why it is so.
After that, you should have three meshes with following mesh elements.
|
Coarse |
Medium |
Fine |
Mesh Elements |
6240 |
14040 |
31590 |
Your mesh should differ slightly from the above table. The mesh properties given to you in this tutorial are of less significant figures. Whereas the meshes used by the author were generated using script with exact accuracy.
Drag Coefficient Comparison
For each mesh, take note of the drag coefficient and compare with each other.
|
Coarse |
Medium |
Fine |
Cd |
2.4981 |
2.4941 |
2.4927 |
% dif |
0.160378 |
0 |
0.056132 |
Pressure Coefficient Comparison
Go to Problem 1