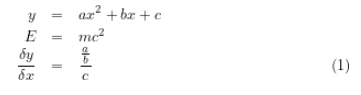Sign-up for free online course on ANSYS simulations!Step 6: Analyze Results
Lift Coefficient
The solution converged after about 480 iterations.
476 1.0131e-06 4.3049e-09 1.5504e-09 6.4674e-01 2.4911e-03 0:00:48 524 ! 477 solution is converged 477 9.9334e-07 4.2226e-09 1.5039e-09 6.4674e-01 2.4910e-03 0:00:38 523
From FLUENT main window, we see that the lift coefficient is 0.647. This compare fairly well with the literature result of 0.6 from Abbott et al.
Plot Velocity Vectors
Let's see the velocity vectors along the airfoil.
Display > Vectors
Enter 4 next to Scale. Enter 3 next to Skip. Click Display.
As can be seen, the velocity of the upper surface is faster than the velocity on the lower surface.
White Background on Graphics Window
To get white background go to:
Main Menu > File > Hardcopy
Make sure that Reverse Foreground/Background is checked and select Color in Coloring section. Click Preview. Click No when prompted "Reset graphics window?"
On the leading edge, we see a stagnation point where the velocity of the flow is nearly zero. The fluid accelerates on the upper surface as can be seen from the change in colors of the vectors.
On the trailing edge, the flow on the upper surface decelerates and converge with the flow on the lower surface.
Do note that the time for fluid to travel top and bottom surface of the airfoil is not necessarily the same, as common misconception
Plot Pressure Coefficient
Pressure Coefficient is a dimensionless parameter defined by the equation
No Latex value
No preview is available, please have your Latex markup text selected when inserting the Latex macro or click edit on an existing Latex macro when text is present to preview the rendered result.
Example Markup
\begin{eqnarray}
y&=&ax^{2}+bx+c \nonumber\\
E&=&mc^2 \nonumber\\
{\delta y \over \delta x}
&=& {{a\over b}\over c}
\end{eqnarray}
Example Render
For more information about Latex, you can find in the following documentation LaTeX Plugin
where p is the static pressure,
Pref is the reference pressure, and
qref is the reference dynamic pressure defined by
No Latex value
No preview is available, please have your Latex markup text selected when inserting the Latex macro or click edit on an existing Latex macro when text is present to preview the rendered result.
Example Markup
\begin{eqnarray}
y&=&ax^{2}+bx+c \nonumber\\
E&=&mc^2 \nonumber\\
{\delta y \over \delta x}
&=& {{a\over b}\over c}
\end{eqnarray}
Example Render
For more information about Latex, you can find in the following documentation LaTeX Plugin
The reference pressure, density, and velocity are defined in the Reference Values panel in Step 5. Please refer to FLUENT's help for more information. Go to Help > User's Guide Index for help.
Plot > XY Plot...
Change the Y Axis Function to Pressure..., followed by Pressure Coefficient. Then, select airfoil under Surfaces.
Click Plot.
The lower curve is the upper surface of the airfoil and have a negative pressure coefficient as the pressure is lower than the reference pressure.
Plot Pressure Contours
Plot static pressure contours.
Display > Contours...
Select Pressure... and Pressure Coefficient from under Contours Of. Check the Filled and Draw Grid under Options menu. Set Levels to 50.
Click Display.
From the contour of pressure coefficient, we see that there is a region of high pressure at the leading edge (stagnation point) and region of low pressure on the upper surface of airfoil. This is of what we expected from analysis of velocity vector plot. From Bernoulli equation, we know that whenever there is high velocity, we have low pressure and vise versa.
Go to Step 7: Refine Mesh