| Panel |
|---|
Problem Specification |
| Info | ||
|---|---|---|
| ||
Click Here for the FLUENT 12 version. |
Step 4: Set Up Problem in FLUENT
If you have skipped the previous mesh generation steps 1-3, you can download the mesh by right-clicking on this link. Save the file as wedge.msh. You can then proceed with the flow solution steps below.
Launch FLUENT
Start > Programs > Fluent Inc > FLUENT 6.3.26
Select 2ddp from the list of options and click Run.
The "2ddp" option is used to select the two-dimensional (2d), double-precision (dp) solver. In the double-precision solver, each floating point number is represented using 64 bits in contrast to the single-precision solver which uses 32 bits. The extra bits increase not only the precision but also the range of magnitudes that can be represented. The downside of using double precision is that it requires more memory.
Import File
Main Menu > File > Read > Case...
Navigate to your working directory and select the wedge.msh file. Click OK.
Check that the displayed information is consistent with our expectations.
Analyze Grid
First, we check the grid to make sure that there are no errors.
Main Menu > Grid > Check
Any errors in the grid would be reported at this time. Check the output and make sure that there are no errors reported.
Grid > Info > Size
How many cells and nodes does the grid have?
Display > Grid
You can look at specific parts of the grid by choosing the items you wish to view under Surfaces (click to select and click again to deselect a specific boundary). Click Display again when you have selected your boundaries. Note what the surfaces farfield, wedge, etc. correspond to by selecting and plotting them in turn.
Define Properties
Define > Models > Solver...
We see that FLUENT offers two methods ("solvers") for solving the governing equations: Pressure-Based and Density-Based. To figure out the basic difference between these two solvers, let's turn to the documentation.
Main Menu > Help > User's Guide Contents ...
This should bring up FLUENT 6.3 User's Guide in your web browser. If not, access the User's Guide from the Start menu: Start > Programs > Fluent Inc Products > Fluent 6.3 Documentation > Fluent 6.3 Documentation. This will bring up the FLUENT documentation in your browser. Click on the link to the user's guide.
Go to chapter 25 in the user's guide; it discusses the Pressure-Based and Density-Based solvers. Section 25.1 introduces the two solvers:
"Historically speaking, the pressure-based approach was developed for low-speed incompressible flows, while the density-based approach was mainly used for high-speed compressible flows. However, recently both methods have been extended and reformulated to solve and operate for a wide range of flow conditions beyond their traditional or original intent."
"In both methods the velocity field is obtained from the momentum equations. In the density-based approach, the continuity equation is used to obtain the density field while the pressure field is determined from the equation of state."
"On the other hand, in the pressure-based approach, the pressure field is extracted by solving a pressure or pressure correction equation which is obtained by manipulating continuity and momentum equations."
Mull over this and the rest of this section. So which solver do we use for our wedge problem? Turn to section 25.7.1 in chapter 25:
"The pressure-based solver traditionally has been used for incompressible and mildly compressible flows. The density-based approach, on the other hand, was originally designed for high-speed compressible flows. Both approaches are now applicable to a broad range of flows (from incompressible to highly compressible), but the origins of the density-based formulation may give it an accuracy (i.e. shock resolution) advantage over the pressure-based solver for high-speed compressible flows."
Since we expect an oblique shock for our problem and the density-based solver is likely to resolve the shock better, let's pick this solver.
In the Solver menu, select Density Based.
Click OK.
Define > Models > Viscous
Select Inviscid under Model.
Click OK. This means the solver will neglect the viscous terms in the governing equations.
Define > Models > Energy
In compressible flow, the energy equation is coupled to the continuity and momentum equations. So we need to solve the energy equation for our problem.
To turn on the energy equation, check the box next to Energy Equation and click OK.
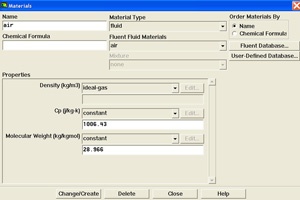
Define > Materials
Make sure air is selected under Fluid Materials. Set Density to ideal-gas and make sure Cp is constant and equal to 1006.43 j/kg-k. Also make sure the Molecular Weight is constant and equal to 28.966 kg/kgmol. Selecting the ideal gas option means that FLUENT will use the ideal-gas equation of state to relate density to the static pressure and temperature.
| newwindow | ||||
|---|---|---|---|---|
| ||||
https://confluence.cornell.edu/download/attachments/90740222/step4_03.jpg?version=1 |
Click Change/Create.
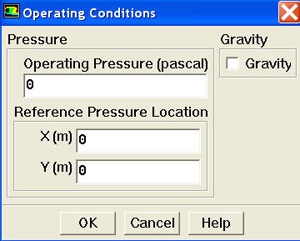
Define > Operating Conditions
To understand what the Operating Pressure is, read through the short-and-sweet section 8.14.2 in the user's guide. We see that for all flows, FLUENT uses the gauge pressure internally in order to minimize round-off errors. Any time an absolute pressure is needed, as in the ideal gas law, it is generated by adding the operating pressure to the gauge pressure:
absolute pressure = gauge pressure + operating pressure
Round-off errors occur when pressure changes Δp in the flow are much smaller than the pressure values p. One then gets small differences of large numbers. For our supersonic flow, we'll get significant variation in the absolute pressure so that pressure changes Δp are comparable to pressure levels p. So we can work in terms of absolute pressure without being hassled by pesky round-off errors. To have FLUENT work in terms of the absolute pressure, set the Operating Pressure to 0.
Thus, in our case, there is no difference between the gauge and absolute pressures. Click OK.
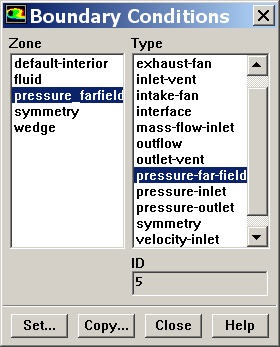
Define > Boundary Conditions
Set the boundary condition for the pressure_farfield surface (aka zone) to the pressure-far-field boundary type by clicking on the latter. Select Yes in the pop-up window asking if it's "OK to change pressure_farfield's type from wall to pressure-far-field?".
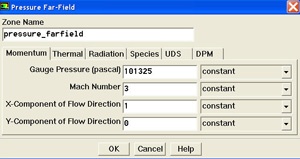
Set the Gauge Pressure to 101325. Set the Mach Number to 3. Under X-Component of Flow Direction, enter a value of 1 (i.e. the farfield flow is in the X direction).
Next, click on the Thermal Tab. Change the temperature to 300K.
| newwindow | ||||
|---|---|---|---|---|
| ||||
https://confluence.cornell.edu/download/attachments/90740222/step4_06.jpg?version=1 |
Click OK. The pressure-far-field boundary type effectively imposes that there is no upstream propagation of disturbances if the flow at the boundary is supersonic. See section 7.9 of the FLUENT help for more details about this boundary type.
Similarly, change the boundary condition for the symmetry surface to the symmetry boundary type. No user input is required for the symmetry boundary type. At any boundary set to the symmetry type, FLUENT internally sets
- normal velocity = 0
- normal gradients of all variables = 0
See section 7.14 of the FLUENT help for more details.
The boundary type for the wedge surface is set to wall by default. There is no need to change that.
Go to Step 5: Solve!
 Sign-up for free online course on ANSYS simulations!
Sign-up for free online course on ANSYS simulations!