...
Pre-Analysis & Start-Up
Pre-Analysis
In the Pre-Analysis step, we'll review the following:
- Mathematical model: We'll look at the governing equations + boundary conditions and the assumptions contained within the mathematical model.
- Numerical solution procedure in ANSYS: We'll briefly overview the solution strategy used by ANSYS and contrast it to the hand calculation approach.
- Hand-calculations of expected results: We'll use an analytical solution of the mathematical model to predict the expected particle velocity at the blade tip. We'll pay close attention to additional assumptions that have to be made in order to obtain an analytical solution.
Mathematical Model
Governing Equations
The governing equations are the continuity and Navier-Stokes equations. These equations are written in a steady rotating frame of reference rotating with the blade. This has the advantage of making our simulation not require a moving mesh to account for the rotation of the blade.
This form of the Navier Stokes equations has additional terms, namely the centripetal acceleration term and the Coriolis term. The equations that we will use looks look as followfollows:
Conservation of mass:
| Latex |
|---|
| Wiki Markup |
{latex} \begin{equation*} \frac{\partial \rho}{\partial t}+\nabla \cdot \rho \vec{v}^{\,}_r =0 \end{equation*} {latex} |
Conservation of Momentum (Navier-Stokes):
| Latex |
|---|
| Wiki Markup |
{latex} \begin{equation*} \nabla \cdot (\rho \vec{v}^{\,}_r \vec{v}^{\,}_r)+\rho(2 \vec{\omega}^{\,} \times \vec{v}^{\,}_r+\vec{\omega}^{\,} \times \vec{\omega}^{\,} \times \vec{r}^{\,})=-\nabla p +\nabla \cdot \overline{\overline{\tau}}_r \end{equation*} {latex} |
Where
Where
| Latex |
|---|
$\vec |
| Wiki Markup |
{latex}$vec{v}^{\,}_r)${latex}r$ |
is is the relative velocity (the velocity viewed from the moving frame) and
| Latex |
|---|
$\vec{\omega}^{\,}$ |
is the angular velocity.
Note the additional terms for the Coriolis force (
| Latex |
|---|
$2 \vec{\omega}^{\,} \times \vec{v}^{\,}_r$ |
) and the centripetal acceleration (
| Latex |
|---|
$\vec{\omega}^{\,} \times \vec{\omega}^{\,} \times \vec{r |
| Wiki Markup |
{latex}$vec{\omega}^{\,}$ |
) in the Navier-Stokes equations. In Fluent, we'll turn on the additional terms for a moving frame of reference and input
| Latex |
|---|
${latex}\vec{\omega}^{\,}= -2.22 \mathbf{\hat{k}}$ |
.
is the angular velocity. For more information about flows in a moving frame of reference, visit ANSYS Help View>Fluent>Theory Guide>2View > Fluent > Theory Guide > 2. Flow in a Moving Frame of Reference and and ANSYS Help Viewer>Fluent>UserViewer > Fluent > User's Guide>9Guide > 9. Modeling Flows with Moving Reference Frames.
Important: We use the Reynolds Averaged form of continuity and momentum and use the SST k-omega turbulence model to close the equation set.
Boundary Conditions
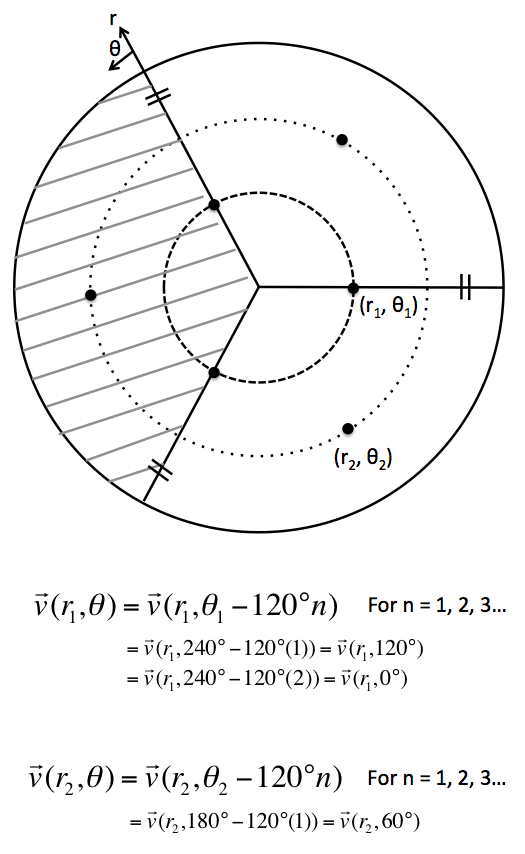
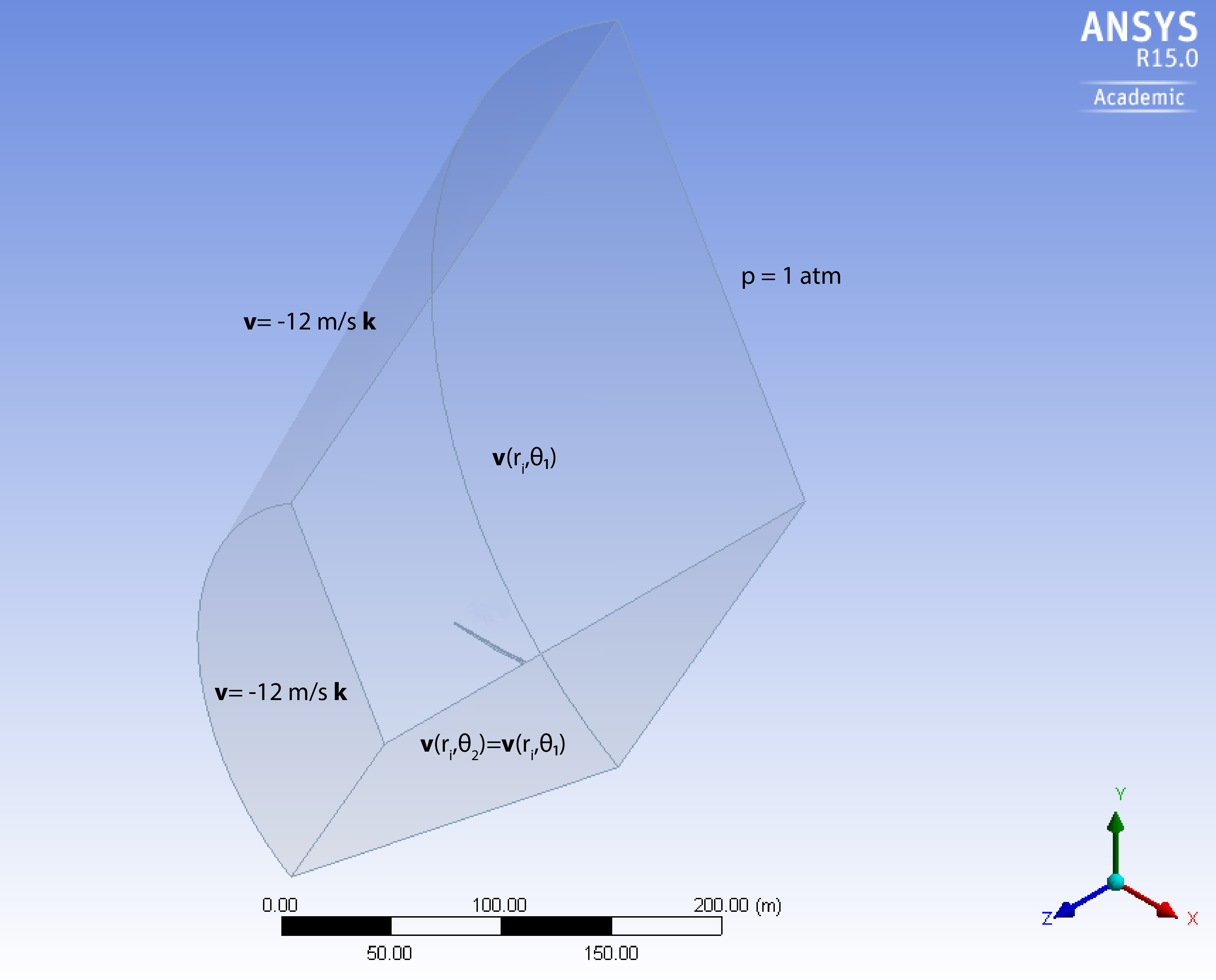
We model only 1/3 of the full domain using periodicity assumptions:
| Latex |
|---|
\begin{equation*}
\vec{v}^{\,}(r_1,\theta) = \vec{v}^{\,}(r_1,\theta_1 - 120n)
\end{equation*}
|
This therefore proves that the velocity distribution at theta of 0 and 120 degrees are the same. If we denote theta_1 to represent one of the periodic boundaries for the 1/3 domain and theta_2 being the other boundary, then
| Latex |
|---|
$\vec{v}^{\,}(r_i,\theta_1)=\vec{v}^{\,}(r_i,\theta_2)$ |
.
...
The boundary conditions on the fluid domain are as follow:
Inlet: Velocity of 12 m/s with turbulent intensity of 5% and turbulent viscosity ratio of 10
Outlet: Pressure of 1 atm
Blade: No-slip
Side Boundaries: Periodic
Numerical Solution Procedure in ANSYS
...
FLUENT converts these differential equations into a set of algebraic equations. Inverting these algebraic equations gives the value of (u, v, w, p, k, omega) at the cell centers. Everything else is derived from the cell centers values (post-processing). In our mesh, we'll have around 400,000 cells. The total number of unknowns and hence algebraic equations is:
400,000 * 6 = 2.4 million.
This huge set of algebraic equations is inverted through an iterative process. The matrix to be inverted is huge but sparse.
In FLUENT, we will use the pressure-based solver.
Hand-Calculations of Expected Results
...
The velocity, v, on the blade should follow the formula
| Latex |
|---|
| Wiki Markup |
{latex} \begin{equation*} v=r \times \omega_{} \end{equation*} {latex} |
| Wiki Markup |
|---|
{latex}
\begin{equation*}
\mathbf{m \ddot{x} + k x =0}
\end{equation*}
{latex} |
| Wiki Markup |
|---|
{latex}
\begin{equation*}
m \ddot{x} + k x =0
\end{equation*}
{latex} |
| Wiki Markup |
|---|
{latex}
\begin{equation*}
\boldsymbol{m \ddot{x} + k x =0}
\end{equation*}
{latex} |
Plugging in our angular velocity of -2.22 rad/s and using the blade length of 43.2 meters plus 1 meter to account for the distance from the root to the hub, we get
| Latex |
|---|
$$v |
| Wiki Markup |
{latex} \begin{equation*} v=-2.22\ \mathrm{rad/s}\ \mathbf{\hat{k}} \times -44.2\ \mathrm{m}\ \mathbf{\hat{i}}$$ \end{equation*} \begin{equation*} v=98.1\ \mathrm{m/s}\ \mathbf{\hat{j}} \end{equation*} {latex} |
Start-Up
*Insert video
It will cover:
-Opening ANSYS
-Setting up the project schematic for the geometry and the Fluid flow, naming them.
$$v=98.12\ \mathrm{m/s}\ \mathbf{\hat{j}}$$
|
Additionally, by using the simple one-dimensional momentum theory, we can estimate the power coefficient which is the fraction of harnessed power to total power in the wind for the given turbine swept area. This analysis uses the following assumptions:
- The flow is steady, homogenous and incompressible.
- There is no frictional drag.
- There is an infinite number of blades.
- There is uniform thrust over the disc or rotor area.
- The wake is non-rotating.
- The static pressure far upstream and downstream of the rotor is equal to the undisturbed ambient pressure.
According to the M.Eng report presented in the problem statement, this blade is meant to ressemble GE 1.5 XLE wind turbine blade. The specification sheet of this turbine states the rated power of this turbine to be 1.5 MW, the rated wind speed to be 11.5 m/s and the rotor diameter to be 82.5 m.
Thus, at rated wind speed,
| Latex |
|---|
\begin{eqnarray*}
C_p = \frac{P_{rated}}{P_{wind}}
= \frac{P_{rated}}{0.5\rho A V_{rated}^3}
= \frac{P_{rated}}{0.5(1.225\frac{kg}{m^3})(\frac{\pi(82.5m)^2}{4})(11.5\frac{m}{s})^3}
= 0.30
\end{eqnarray*}
|
The resulting power coefficient of 0.30 is very reasonable. We will compare it to power coefficient obtained from the simulation in the Verification & Validation section.
...
Start-Up
Please follow along to start this project! It is recommended to have these videos run side by side with your ANSYS project, with the video taking 1/3 of the screen space and the ANSYS window taking 2/3 of the screen space. An even better method is to use two monitors. This would allow running both the tutorial videos and ANSYS in full-screen. For example, the tutorial would be opened up on your laptop and ANSYS would be running on a lab computer. If you use the Cornell lab computers then make sure to bring some earbuds!
| HTML |
|---|
<iframe width="640" height="360" src="//www.youtube.com/embed/paSsU19hNy0" frameborder="0" allowfullscreen></iframe> |
Summary of the above video:
- Open up ANSYS Workbench
- Drag Fluid Flow (Fluent) from Analysis Systems into Project Schematic
- Rename Project
- Save Project
...
 Sign-up for free online course on ANSYS simulations!
Sign-up for free online course on ANSYS simulations!