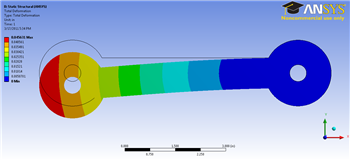
First, we will look at the deformation to see if the simulation makes intuitive sense. In the project outline window, select Solution > Total Deformation. Also, in the Result tool bar, select Edges > Show Undeformed WireFrame.

From the deformed view, we can see that the crank deformed basically as we would expect from this loading.
Now, let's examine the strain at the strain gauge. If we select Solution > Normal Elastic Strain we can see the strain distribution along the path we created. In the Tabular Data window, we can see the numerical values of the strain along the path.
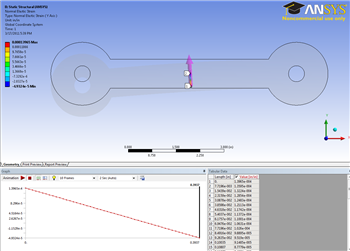
While the strain along the entire strain gauge is useful, what we really want is the average along the strain gauge. Right click anywhere in tabular data window, and go to Export. Save the file as an .xls file and name it Strain data. Open the file, and average the data by selecting all of the strain data, then going to Formulas > AutoSum > Average. At the bottom of the data, we will see the calculated average of the strain gauge: 4.5167E-5 in/in.
Strain Gauge Technique Comparison
There are multiple ways to model a strain gauge in ANSYS
1. Creating a small area gauge of zero thickness and zero stiffness
2. Creating a path and averaging the strain values across it
3. Creating a path and calculating strain from the change in length
4. Finding the displacements of two nodes and using this to calculate strain
All four methods were used to measure strain in both the X and Y directions at the same position on the bicycle crank. Results are as follows:
Strain Values:
|
Area Gauge |
Line Strain |
Strain from Line Displacement |
Strain from Nodal Displacement |
X-Strain (Micro-Strain) |
787.17 |
758.93 |
785.71 |
770 |
Y-Strain (Micro-Strain) |
-251.99 |
-251.65 |
-250.00 |
-260 |
Percent Differences using Area Gauge as the base-line:
|
Line Strain vs. Area Gauge |
Line Displacement vs. Area Gauge |
Nodal Displacement vs. Area Gauge |
X-Strain (Micro-Strain) |
-3.59% |
.185% |
2.18% |
Y-Strain (Micro-Strain) |
.135% |
.790% |
3.18% |
Theoretical and Experimental* Values at the Same Position:
|
Experimental (ARAMIS) |
Theory |
X-Strain (Micro-Strain) |
932 |
789.13 |
Y-Strain (Micro-Strain) |
-153 |
-260.41 |
*Experimental data was obtained from using digital image correlation using ARAMIS software. See Verification and Validation section for details.
There is no significant difference between the results of the different methods. All four techniques output acceptable results in both the X and Y directions with only a maximum of a three percent difference between using any of the methods. The Y direction has a slight discrepancy from the experimental values, but this can be explained from an unexpected difference in material properties (see Verification and Validation section).
The procedure for using the area gauge is much more lengthy and complicated than the other three; however, the area gauge allows for strain measurements in cross-wise directions, not along the X, Y, or Z axes, and no further calculations are needed after ANSYS solves the model. The two methods which use paths are both fast and easy to set up, and the gauge can be modified while in the Mechanical workspace. The two path methods both involve calculations after ANSYS completes the solution, though, and the paths will only give solutions in the X, Y, or Z directions. The nodal displacement technique is the most unwieldy, and heavily depends on the mesh of the part. There need to be two nodes along a horizontal or vertical line which are in the region where strain is to be desired. The nodal displacement also requires calculations.
The area strain gauging technique allows for the greatest flexibility in the measurement of the strains. Any direction can be calculated. The line strain gauges are much easier to set up, though, and so if strain is only needed in one of the axis directions, as in this tutorial, these are a good substitute to the area gauge.
For a more details on the analysis of strain gauge techniques see ANSYS Strain Gauge Techniques Report.doc
Now, let's check the stress at the strain gauge. Click on Solution > StressXX in the Project Outline window. This will bring up the stress distribution over the entire crank.
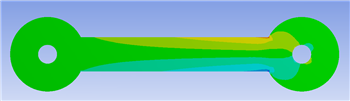
Now, click on the probe tool  Hover the probe tool around where the strain gauge is located. We just want to compare the stresses we see to the calculated value of -1368.65 psi. If you hover the probe around that area, you should find that the stresses are about what we expect them to be based on the calculation. Repeat this step for Solution > StressYY
Hover the probe tool around where the strain gauge is located. We just want to compare the stresses we see to the calculated value of -1368.65 psi. If you hover the probe around that area, you should find that the stresses are about what we expect them to be based on the calculation. Repeat this step for Solution > StressYY

Here, we assumed that the stress was zero. If we use the probe tool to examine the middle section of the bar, we find that most of the stresses are on the order of 1 x 10^-3, meaning once again the simulation agrees with our calculations.
Continue to Step 7: Verification & Validation
Go to all ANSYS Learning Modules
See and rate the complete Learning Module