Step 8: Postprocess the results
Enter the postprocessing module to analyze the solution.
Main Menu > General Postproc
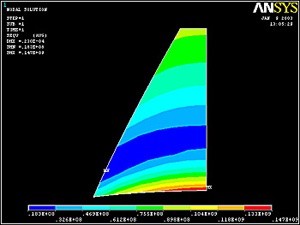
Plot von Mises Stress
To display the von Mises stress distribution as continuous contours, select
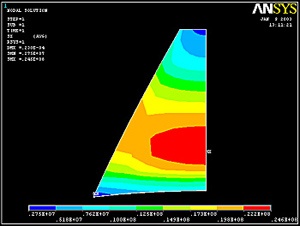
Main Menu > General Postproc > Plot results > Contour Plot > Nodal Solu
Select Stress from the left list, von Mises SEQV from the right list and click OK.
Utility Menu > PlotCtrls > Pan,Zoom,Rotate > Right
(Click Picture for Larger Image)
The maximum von Mises stress is 147 MPa and occurs at the bottom on the symmetry line.
Plot Circumferential Stress
σθis the SY stress component in cylindrical coordinates in ANSYS. Activate the cylindrical coordinate system for results display (you need to do this even if you were working in the cylindrical system in the preprocessor):
Main Menu > General Postproc > Options for Outp
Select Global Cylindric for Results Coord System.
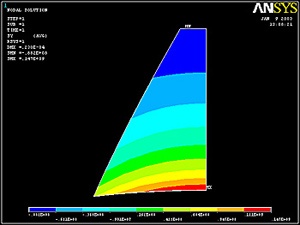
To display theσθstress distribution over face 1 as continuous contours, select
Utility Menu > PlotCtrls > Pan,Zoom,Rotate > Right
Main Menu > General Postproc > Contour Plot > Plot results > Nodal Solu
Select Stress from the left list, Y-direction SY from the right list and click OK.
(Click Picture for Larger Image)
Check where the maximum (MX) and minimum (MN) σθvalues occur in the plot. The circumferential stress is tensile (positive) and compressive (negative) on the inner and outer portions of the cross-section, respectively. Is this what you'd have expected? Theσθcontours are more closely spaced at smaller r values. This agrees with the prediction of curved beam theory that the stress gradients will be highest on the edge nearest the center of curvature.
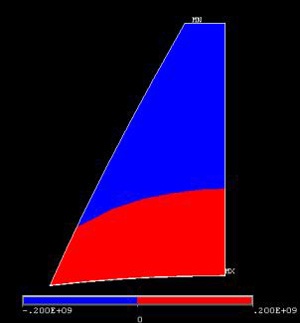
Plot Neutral Axis
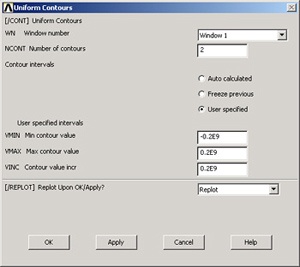
The neutral axis is the locus of points where σθis zero. To visualize the neutral axis, we'll change the contour levels that are plotted.
Utility Menu > PlotCtrls > Style > Contours > Uniform Contours
Enter 2 for Number of contours, and choose User specified for Contour Intervals. Enter Min contour value=-0.2E9, Max contour value=0.2E9, and Contour value incr=0.2E9. Click OK.
This plots the regions with positive and negative σθvalues in different colors. In the red region, 0<σθ<200MPa and in the blue region, -200MPa<σθ<0. So the boundary between the two colors is the neutral axis.
The FEA results indicate that the neutral axis is curved, contrary to the assumption in mechanics of materials theory.
Plot Radial Stress
In cylindrical coordinates, the radial stress is the SX stress component.
Main Menu > General Postproc > Plot results > Nodal Solu...
Select Stress from the left list, X-direction SX from the right list and click OK.
Change contour plot options back to original:
Utility Menu > PlotCtrls > Style > Contours > Uniform Contours
Enter 9 for Number of Contours, and choose Auto calculated for Contour Intervals. Click OK.
(Click Picture for Larger Image)
The radial stress is tensile over the entire cross-section.
Plot Deformed Shape
Main Menu > General Postproc > Plot Results > Deformed Shape
Select Def + undeformed and click OK.
This plots the deformed and undeformed shapes in the Graphics window. The maximum displacement DMX=0.230e-4 m.
Animate the deformation:
Utility Menu > PlotCtrls > Animate > Deformed Shape
Select Def + undeformed and click OK. Select Forward Only in the Animation Controller.
From the animation of the deformation of the cross-section, check that the following BCs are satisfied: u=0 at node A, w=0 along AB and CD. (Note that the z-direction is from right to left in the above view).
The radial stress is tensile, so the radial dimension becomes larger as expected. We saw that the circumferential stress is, respectively, tensile and compressive on the inner and outer portions of the cross-section. You can check that the stress SZ parallel to the axis of revolution is small. Therefore, the Poisson effect should cause the inner and outer portions, respectively, to contract and expand in the z-direction as is observed. Circumferential tension on the inner portion pulls material toward the center of curvature. Outer corners are more flexible than the central portion. So it makes sense that the outer, bottom corner moves inward with respect to central point A (Cook et al). Thus, the deformation we gets looks reasonable.
Animate the front view:
Utility Menu > PlotCtrls > Pan,Zoom,Rotate > Front
Utility Menu > PlotCtrls > Animate > Deformed Shape
Select Def + undeformed and click OK. Select Forward Only in the Animation Controller.
From this animation, check that the BCs for v on both faces are satisfied.
Save your work: Toolbar > SAVE_DB
Go to Step 9: Validate the results
 Sign-up for free online course on ANSYS simulations!
Sign-up for free online course on ANSYS simulations!