A Differential relates the angular positions and forces of three gears on a common axis of rotation. They are commonly used in car steering systems to make sure that when a car rounds a corner, the inside wheel spins less than the outside wheel. In our erg, we use the differential to split an input force from the handle to the two output forces that act on flywheel and the tires.
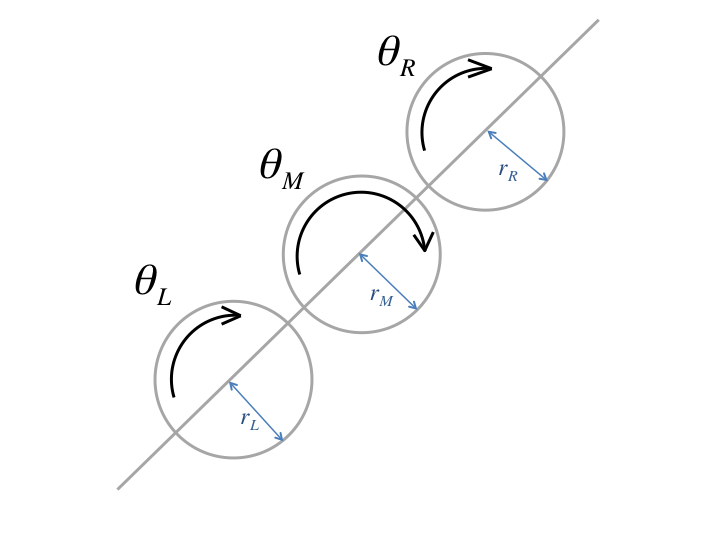
Subscripts
correspond the left half-shaft, right half-shaft, and middle gear, respectively.Three observations:
- When we hold the right axle fixed and turn the left axle one revolution, the middle sprocket makes half a revolution in the same angular direction.
- Holding the middle sprocket in place and turning the left axle one revolution causes the right axle to make one revolution in the opposite direction.
- The above observations are the same if the left and right axle are switched.
The results can be summarized as such:
| Latex |
|---|
\large\begin{align*}
\theta_{\text{M}} = \frac{1}{2}\theta_{\text{L}} + \frac{1}{2}\theta_{\text{R}}
\end{align*}
|
where
represents angular position. In other words, the
position of the middle gear is half the sum of the left and right gears. Say that
represents angular velocity,
represents angular acceleration, and
represents torque.
is the radius of the gear, and
is the linear velocity at the edge of a gear. From the first equation, we can find the relationships between the angular and linear velocities of the gears.
| Latex |
|---|
\large
\begin{align*}
\omega_{\text{M}} =& \frac{1}{2} \left( \omega_{\text{L}} + \omega_{\text{R}} \right)
\\
\omega_{\text{M}} r_{\text{M}} =& \frac{1}{2} ( \omega_{\text{L}} r_{\text{M}} +
\omega_{\text{R}} r_{\text{M}})
\\
v_{\text{M}} =& \frac{1}{2} \left( \omega_{\text{L}} r_{\text{M}} \frac{r_{\text{L}}}{r_{\text{L}}} +
\omega_{\text{R}} r_{\text{M}} \frac{r_{\text{R}}}{r_{\text{R}}} \right)
\\
v_{\text{M}} =& \frac{1}{2} \left( v_{\text{L}} \frac{r_{\text{M}}}{r_{\text{L}}} +
v_{\text{R}} \frac{r_{\text{M}}}{r_{\text{R}}} \right)
\end{align*}
|
We assume that these ideal gears are frictionless and massless. Therefore, we can use conservation of energy to say that input power equals output power. Say
represents power as a function of time.
| Latex |
|---|
\large
\begin{align*}
&P_{\text{M}} = P_{\text{L}} + P_{\text{R}} \\
&\tau_{\text{M}} \cdot \omega_{\text{M}} = \tau_{\text{L}} \cdot \omega_{\text{L}} +
\tau_{\text{R}} \cdot \omega_{\text{R}} \\
&\tau_{\text{M}} \cdot \left[ \frac{1}{2} \left( \omega_{\text{L}} + \omega_{\text{R}} \right) \right]
= \tau_{\text{L}} \cdot \omega_{\text{L}} +
\tau_{\text{R}} \cdot \omega_{\text{R}}
\end{align*}
|
If we consider
| Latex |
|---|
\large $\omega_{\text{L}}$ |
and
| Latex |
|---|
$\omega_{\text{R}}$ |
separately, we find that
| Latex |
|---|
\large
\begin{align*}
\frac{1}{2} \tau_{\text{M}} \omega_{\text{L}} &= \tau_{\text{L}} \omega_{\text{L}}, \;\;\;
\frac{1}{2} \tau_{\text{M}} \omega_{\text{R}} = \tau_{\text{R}} \omega_{\text{R}}
\\
\frac{1}{2} \tau_{\text{M}} &= \tau_{\text{L}}, \;\;\;\;\;\;\; \;\; \; \;\; \frac{1}{2} \tau_{\text{M}} = \tau_{\text{R}}
\end{align*}
|
Therefore, we can conclude that the relationships between torques is the same as the relationships between angular position; a torque on the middle gear is evenly divided between the torque on the left gear and the torque on the right gear.
| Latex |
|---|
\large
\begin{align*}
\tau_{\text{M}} &= \tau_{\text{L}} + \tau_{\text{R}} \\
\tau_{\text{L}} &= \tau_{\text{R}} = \frac{1}{2} \tau_{\text{M}}
\end{align*}
|
Prof Ruina's favorite video on how a differential works
| Widget Connector |
|---|
| url | http://www.youtube.com/watch?v=yYAw79386WI |
|---|
|
